Author(s):
(1) Irene Drelichman, member of CONICET, Argentina.
Content Overview
Abstract & Introduction
Notation and Preliminary Results
Proof of our main theorem
Applications to fractional Poincar´e inequalities
References
Abstract.
We characterize the real interpolation space between weighted L1 and W1,1 spaces on arbitrary bounded domains, when the weights are positive powers of the distance to the boundary multiplied by an A1 weight. As an application of this result we obtain weighted fractional Poincar´e inequalities with sharp dependence on the fractional parameter s (for s close to 1) and show that they are equivalent to a weighted Poincar´e inequality for the gradient.
1. Introduction


2. Notation and Preliminary Results



3. Proof of our main theorem





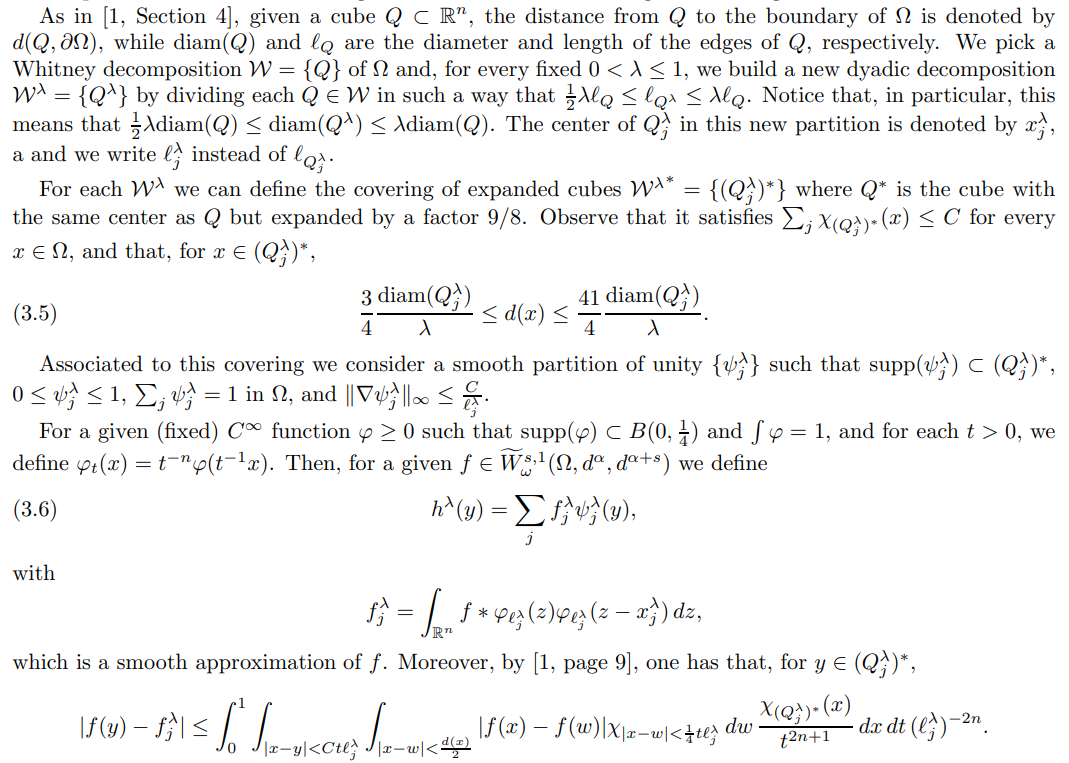
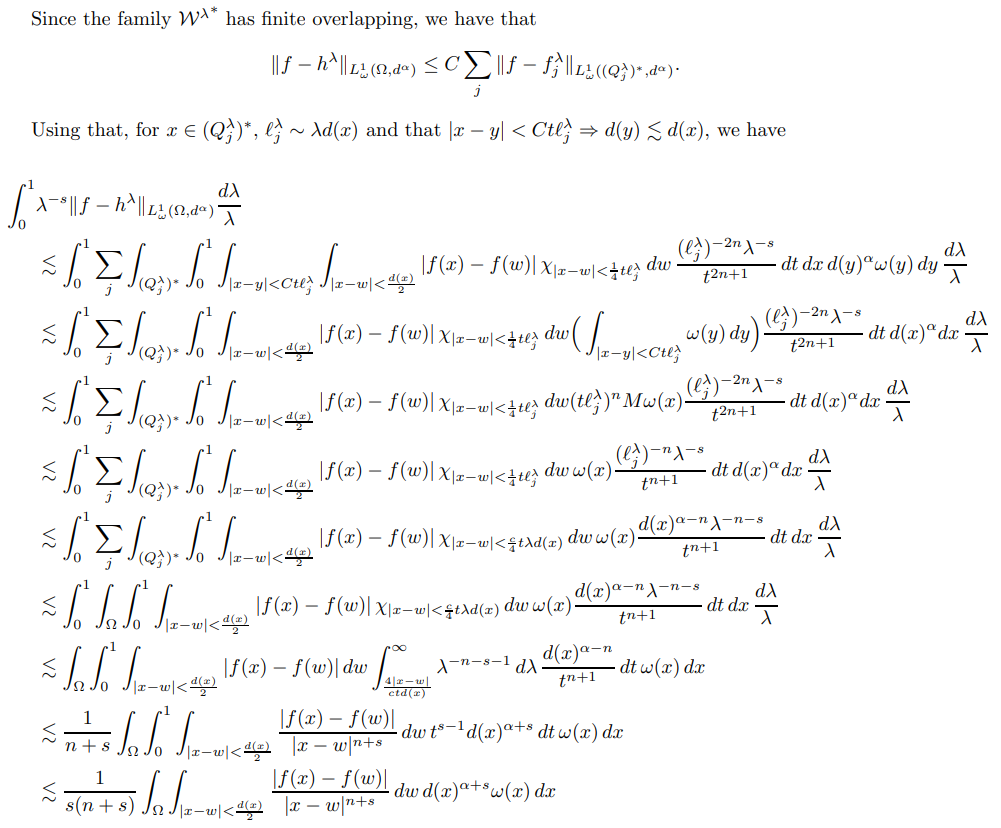
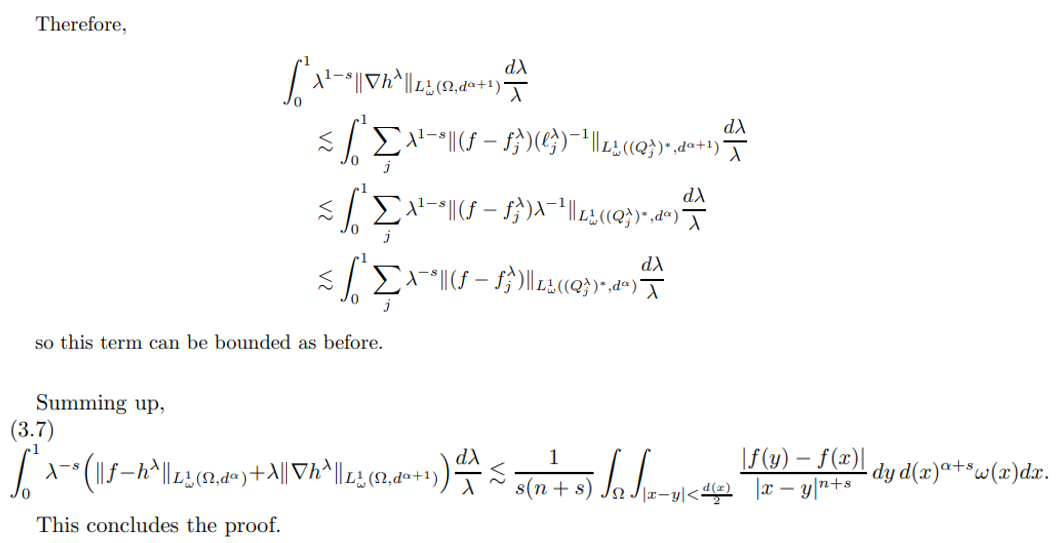
4. Applications to fractional Poincar´e inequalities
In the forthcoming results we will make use of two well-known properties of weighted norms contained in the following lemma. We include a proof for the sake of completeness.

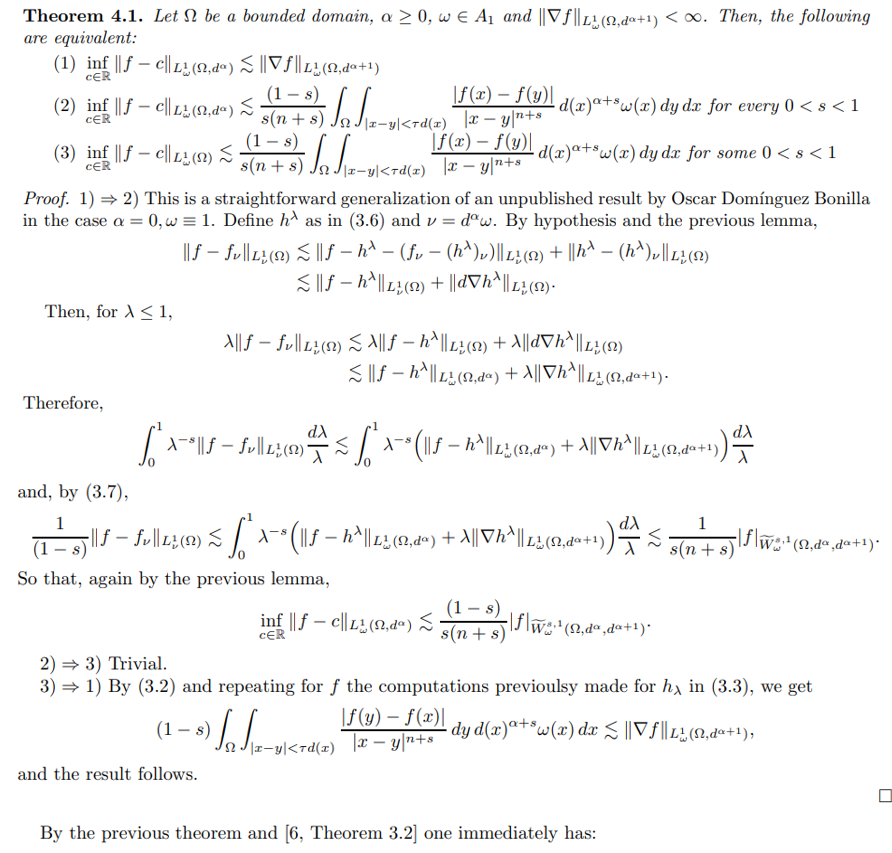

References
[1] Acosta, G.; Drelichman, I.; Dur´an, R.G. Weighted fractional Sobolev spaces as interpolation spaces in bounded domains. Math. Nachr. 296 (2023), no. 9, 4374–4385.
[2] Brezis, H. How to recognize constant functions. A connection with Sobolev spaces. Russian Math. Surveys 57 (2002), no. 4, 693–708
[3] Bourgain, J.; Brezis, H.; Mironescu, P. Another look at Sobolev spaces. Optimal control and partial differential equations, IOS, Amsterdam, 2001, pp. 439–455.
[4] Bourgain, J.; Brezis, H.; Mironescu, P. Limiting embedding theorems for Ws,p when s ↑ 1 and applications. J. Anal. Math. 87 (2002), 77–101.
[5] Drelichman, I.; Dur´an, R. G. Improved Poincar´e inequalities in fractional Sobolev spaces. Ann. Acad. Sci. Fenn. Math. 43 (2018), no. 2, 885–903.
[6] Drelichman, I.; Dur´an, R. G. Improved Poincar´e inequalities with weights. J. Math. Anal. Appl. 347 (2008), no. 1, 286–293.
[7] Drelichman, I.; Dur´an, R. G. The Bourgain-Br´ezis-Mironescu formula in arbitrary bounded domains. Proc. Amer. Math. Soc. 150 (2022), no. 2, 701–708.
[8] Dyda, B.; Ihnatsyeva, L.; V¨ah¨akangas, A. V. On improved fractional Sobolev-Poincar´e inequalities. Ark. Mat. 54 (2016), no. 2, 437–454.
[9] Gogatishvili, A.; Koskela, P.; Shanmugalingam, N. Interpolation properties of Besov spaces defined on metric spaces. Math. Nachr. 283 (2010), no. 2, 215–231.
[10] Guo, CY. Fractional Sobolev-Poincar´e inequalities in irregular domains. Chin. Ann. Math. Ser. B 38 (2017), 839–856 .
[11] Hedberg, L. I. On certain convolution inequalities. Proc. Amer. Math. Soc. 36 (1972), 505–510.
[12] Hurri-Syrj¨anen, R.; V¨ah¨akangas, A. V. On fractional Poincar´e inequalities. J. Anal. Math. 120 (2013), 85–104.
[13] Jiang, R.; Kauranen, A.; Koskela, P. Solvability of the divergence equation implies John via Poincar´e inequality. Nonlinear Anal. Theory Methods Appl. 101 (2014), 80–88.
[14] Myyryl¨ainen, K., P´erez, C., Weigt, J. Weighted Fractional Poincar´e inequalities via isoperimetric inequalities. arXiv:2304.02681v2 (2023).
[15] Maz’ya, V.; Shaposhnikova, T. On the Bourgain, Brezis, and Mironescu theorem concerning limiting embeddings of fractional Sobolev spaces. J. Funct. Anal. 195 (2002), no. 2, 230–238.
[16] Milman, M. Notes on limits of Sobolev spaces and the continuity of interpolation scales. Trans. Amer. Math. Soc. 357 (2005), no. 9, 3425–3442
[17] Mohanta, K. Bourgan-Br´ezis-Mironescu formula for Triebel-Lizorkin spaces in arbitrary domains. arXiv:2308.12830v2 (2023).
[18] Muckenhoupt, B. Weighted norm inequalities for the Hardy maximal function. Trans. Amer. Math. Soc. 165 (1972), 207–226.
[19] L´opez-Garc´ıa, F.; Ojea, I. Some inequalities on weighted Sobolev spaces, distance weights and the Assouad dimension. arXiv:2210.12322 (2022).
[20] Ponce, A.C. An estimate in the spirit of Poincar´e’s inequality. J. Eur. Math. Soc. (JEMS) 6 (2004), no. 1, 1–15.
This paper is available on arxiv under CC 4.0 license.

