This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Thomas Pethick, EPFL (LIONS) [email protected];
(2) Wanyun Xie, EPFL (LIONS) [email protected];
(3) Volkan Cevher, EPFL (LIONS) [email protected].
Table of Links
- Abstract & Introduction
- Related work
- Setup
- Inexact Krasnosel’ski˘ı-Mann iterations
- Approximating the resolvent
- Last iterate under cohypomonotonicity
- Analysis of Lookahea
- Experiments
- Conclusion & limitations
- Acknowledgements & References
5 Approximating the resolvent


This can be approximated with a fixed point iteration of
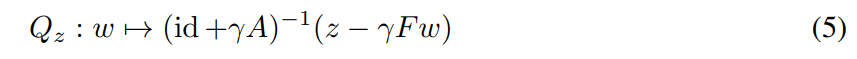
which is a contraction for small enough γ since F is Lipschitz continuous. It follows from Banach’s fixed-point theorem Banach (1922) that the sequence converges linearly. We formalize this in the following theorem, which additionally applies when only stochastic feedback is available.
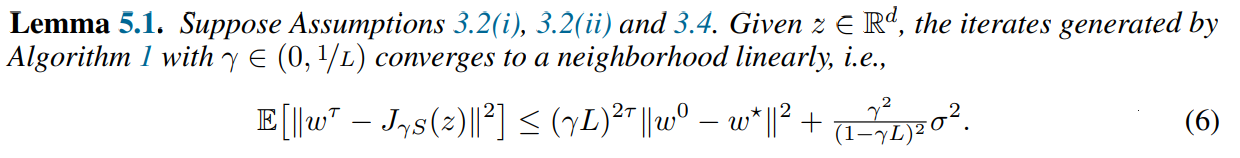
The resulting update in Algorithm 1 is identical to GDA but crucially always steps from z. We use this as a subroutine in RAPP to get convergence under a cohypomonotone operator while only suffering a logarithmic factor in the rate.