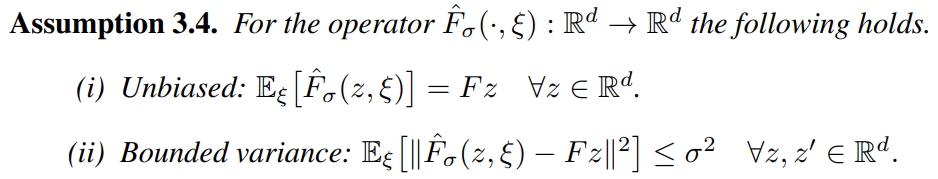This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Thomas Pethick, EPFL (LIONS) [email protected];
(2) Wanyun Xie, EPFL (LIONS) [email protected];
(3) Volkan Cevher, EPFL (LIONS) [email protected].
Table of Links
- Abstract & Introduction
- Related work
- Setup
- Inexact Krasnosel’ski˘ı-Mann iterations
- Approximating the resolvent
- Last iterate under cohypomonotonicity
- Analysis of Lookahea
- Experiments
- Conclusion & limitations
- Acknowledgements & References
3 Setup

Most relevant in the context of GAN training is that (1) includes constrained minimax problems.
Example 3.1. Consider the following minimax problem


We will rely on the following assumptions (see Appendix B for any missing definitions).
Assumption 3.2. In problem (1),

Remark 3.3. Assumption 3.2(iii) is also known as |ρ|-cohypomonotonicity when ρ < 0, which allows for increasing nonmonotonicity as |ρ| grows. See Appendix B.1 for the relationship with weak MVI.
When only stochastic feedback Fˆ σ(·, ξ) is available we make the following classical assumptions.